3. Sınıf Matematik Dersi Nokta - Doğru - Doğru Parçası ? Işın - Düzlem
3. Sınıf Matematik Dersi Nokta - Doğru - Doğru Parçası – Işın - Düzlem
NOKTA
• Duvara çakılan çivinin bıraktığı iz,
• Yüzümüzdeki ben,
• Kalemin ucunun kâğıda bıraktığı iz,
• Tebeşirin tahtaya bıraktığı iz,
• Su damlası,
• Cümlenin bittiğini göstermek için kullanılan işaret noktaya birer örnektir.
• Nokta, büyük temel harflerle adlandırılır.
•A •B •C •K •Y
- Noktanın eni, boyu ve yüksekliği yoktur.
- Nokta (•) işareti ile gösterilir.
- Bir noktadan sınırsız sayıda doğru geçer.

İki sokağın birleştiği yer de bir noktadır.
Harita üzerinde il ilçe merkezleri noktalarla belirtilir.
Saat üzerinde saat başları nokta ile belirtilir.
DOĞRU
Her iki yönden sonsuza kadar giden aynı doğrultudaki noktaların birleşimine doğru denir.
• Doğrunun belirli bir kalınlığı yoktur, sadece uzunluğu vardır.
• Başlangıç ve bitiş noktası yoktur.
• Gergin durumdaki hortum, yol doğru modelidir.
• Doğrular, küçük harflerle ya da iki büyük harfle isimlendirilir.

DOĞRU PARÇASI
İki nokta arasında bulunan tüm noktaların birleşimine doğru parçası denir.
• Doğru parçasının başlangıç ve bitiş noktası bellidir.
• Doğru parçası iki ucundan da uzatılamaz.
Ucu açılmamış kurşun kalem, çubuk makarna birer doğru parçası modelidir.

IŞIN
Bir ucu sınırlı bir ucu sınırsız olan doğrulara ışın denir.
• Işınların başlangıç noktası bellidir ve bir uçundan sınırsız uzatılabilir.
• Televizyon anteni, çelik metre, birer ışın modelidir.
• Işınlar büyük harflerle isimlendirilirler.

DOĞRULARIN ÇEŞİTLERİ
Doğrular yatay doğru, dikey doğru ve eğik doğru olmak üzere üç çeşittir.
Yatay Doğru
Dikey Doğru
Eğik Doğru

DOĞRULARIN DURUMLARI
İki doğrunun durumu paralel, kesişen ve dik doğrular olabilir.
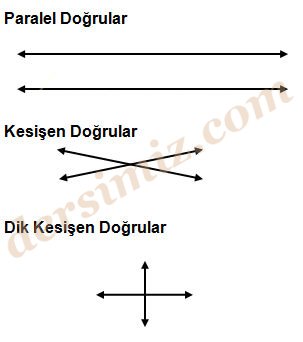
1) Paralel Doğrular: İki doğru hiçbir noktada kesişmiyorsa bu doğrulara paralel doğrular denir.
2) Kesişen Doğrular: İki doğru, bir noktada kesişebilir. Bu doğrulara kesişen doğrular denir.
3) Dik Kesişen Doğrular: Kesişen doğrular birbirini dik kesiyorsa böyle doğrulara dik kesişen doğrular denir.
DÜZLEM
Düzlem bir noktalar kümesidir. Düzlem sınırsızdır. Köşesi ve kenarı yoktur. Sınıf tahtasının yüzeyini, cam yüzeyini, evimizin tabanını düzlem olarak alabiliriz. 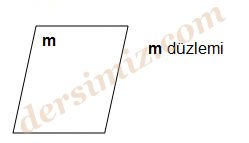
Düzlemler küçük harfle ifade edilirler. Örneğin şekildeki düzlem “m” ile gösterilmiştir. “m” düzlemi
Ekleyen : Ahmet Güloğlu